Exam 2 revision

Section A:

Expected value of $X$	a. $E(X - \mu)$
Variance of $X$	b. $10X$
Standard deviation of $X$	c. $\frac{(X-0.04)}{\sigma}$
Shorthand notation for $P(X=x)$	d. $X+10$
Has 10 times the standard deviation of $X$	e. $E(X-\mu)^2$
Is always equal to zero	f. $\sqrt{VarX}$
Increases the mean of $X$ by 10	g. $\mu$
Has standard deviation 1	h. $p(x)$

Please review AE-8, the solutions are on the Canvas page.

Section B:

Consequence of covariance	a. $p(x,y)$
Covariance between $X$ and $Y$	b. $\rho$
Property of uncorrelated random variables	c. $p(x, y) = p(x)p(y)$
Weighted sum of two random variables	d. $\rho\sigma_x\sigma_y$
Sharpe ratio of random variable	e. $Var(X+Y) >Var(X) + Var(Y)$
Implies $X$ and $Y$ are independent random variables	f. $p(x) = p(y)$
Implies $X$ and $Y$ are identically distributed	g. $X_1, X_2, X_3$
Symbol for the correlation between random variables	h. $Var(X+Y) = Var(X) + Var(Y)$
Symbol for joint probability distribution	i. $S(Y)$
Sequence of iid random variables	j. $3X-2Y$

Please review AE-9, the solutions are on the Canvas page.

Section C:

$Y$ is a binomial random variable with parameters $n$ and $p$, $X$ is a Poisson random variable with parameter $\lambda$ and $B_1$ and $B_2$ are Bernoulli trials with probability of success $p$.

1. Expresssion for the variance of $Y$	a. $np$
Probability that the first trial $B_1$ fails	b. $e^{-\lambda}$
Expression for the mean of $X$	c. $e^{-\lambda} \frac{\lambda^2}{2}$
Probability that $Y$ is zero	d. $p$
Probability that $X$ is 2	e. $0$
Covariance between $B_1$ and $B_2$	f. $p^n$
Expression for the expected value of $X$	g. $1-p$
The expected value of $B_1$	h. $(1-p)^n$
Probability that $Y$ is $n$	i. $np(1-p)$
Probability that $X$ is $0$.	j. $\lambda$

An auditor inspects 25 transactions processed by the business office of a company. The auditor selects these transactions at random from the thousands that were processed in the most recent three months. In the past, the auditor has found 10% of transactions at this type of company to have been processed incorrectly. True or False: A binomial model would be more appropriate for this problem if the auditor picked the first 25 transactions during the three-month period.
Is the binomial model suited to these applications?
1. The next five cars that enter a gasoline filling stations get a fill-up.
2. A poll of the 15 members of the board of directors indicates that 6 are in favor of a proposal to change the salary of the CEO.
3. A company realizes that 10% of its packages are not being sealed properly. When examining a case of 24, it counts the number that are unsealed.
Every now and then even a good diamonds cutter has a problem and the diamond shatters when being cut. For one cutter, the chance of such errors is 0.1%.
1. What is the probability model seems well suited to this problem? Why?
2. If this cutter works on 75 stones, what is the probability that he breaks 2 or more?
A dairy farmer accidentally allowed some of his cows to graze in a pasture containing weeds that would contaminate the milk from his herd. The farmer estimates that there’s a 10% chance of a cow grazing on some of the flavorful weeds.
1. Under these conditions, what is the probability that none of the 12 animals in this herd ate the weeds.
2. Does the poisson model give a good estimate of the probability that no animal ate the weeds?

Section D:

$X$ denotes a normally distributed random variable: $X \sim N(\mu, \sigma^2)$. A googol, the namesake of Google, is $10^{100}$. The random variable $Z$ denotes a standard normal random variable, $Z \sim N(0,1)$

Mean of $X$	a. $\frac{1}{2}$
Variance of $X$	b. $P(Z<1)$
Probability of $X$ being less than its mean	c. $0.05$
Probability of $X$ being less than $\mu +\sigma$	d. $\frac{2}{3}$
Standard deviation of $Z$	e. $\frac{1}{1 googol}$
Probability that a $z-score$ based on $X$ is less than $1$ in magnitude	f. $\mu$
Proportion of a normal distribution that is more than $20\sigma$ from $\mu$	g. $\sigma^2$
Difference between value of $P(Z<-x)$ and value of $P(Z>x)$	h. $1$
Distribution of the random variable $\mu +\sigma Z$	i. $0$
Probability that $Z>1.96$ plus the probability that $Z<-1.96$	j. $N(\mu, \sigma^2)$

The currently age (in years) of 400 clerical employees at an insurance claims processing center is normally distributed with mean 38 and SD 6. True or False: A training program for employees under the age of 30 at the center would be expected to attract about 36 employees.
If $X_1 \sim N(\mu, \sigma)$ and $X_2 \sim N(\mu, \sigma)$ are iid, then what is the distribution of $\frac{X_1-X_2}{\sqrt{2}\sigma}$
A contractor built 30 similar homes in a suburban development. The homes have comparable size and amenities, but each has features that customize the appearance, landscape, and interior. The contractor expects the homes to sell for $450,000. He expects that one-third of the homes will sell either for less than $400,000 or more than $500,000.
1. Would a normal model be appropriate to describe the distribution of sale prices?
2. What data would help you decide if a normal model is appropriate? (These homes are unsold, their prices are unavailable)
3. What normal model has properties that are consistent with the intuition of the contractor?
A hurricane bond pays the holder a face amount, say $1 million, if a hurricane causes major damage in the United States. Suppose that the chance for such a storm is 5% per year.
1. If a financial firm sells these bonds for $60,000, what is the chance that the firm loses money if it only sells one?
2. If the firm sells 1,000 of these policies, each for $60,000, what is the probability that it loses money.
3. How does the difference between the probabilities of parts a and b compare to the situation of an insurance company that writes coverage to homeowners who have accidents independently of one another?

Section E:

Sample	a. A complete collection of items desired to be studied
Census	b. A list of all the items in the population
Target population	c. A subset of a larger collection of items
Statistic	d. A homogeous subset of the population
Parameter	e. A characteristic of a sample
Sampling frame	f. Occurs if a sampling method distorts a property of the population
Simple random sample	g. A comprehensive study of every item of the population
Stratum	h. The result if a respondent chooses not to answer a question
Bias	i. A characteristic of a population
Nonresponse	j. Sample chosen so that all subset of size $n$ are equally likely.

True or False: Bias due to the wording of questions causes different samples to present different impressions of the population.
A school district has requested a survey be conducted on the socioeconomic status of their students. Their budget only allows them to conduct the survey in some of the schools, hence they need to first sample a few schools. Students living in this district generally attend a school in their neighbourhood. The district is broken into many distinct and unique neighbourhoods, some including large single-family homes and others with only low-income housing. What kind of sampling did they employ?

Section F:

Which of the following $X$-bar charts indicate a process that is out of control?
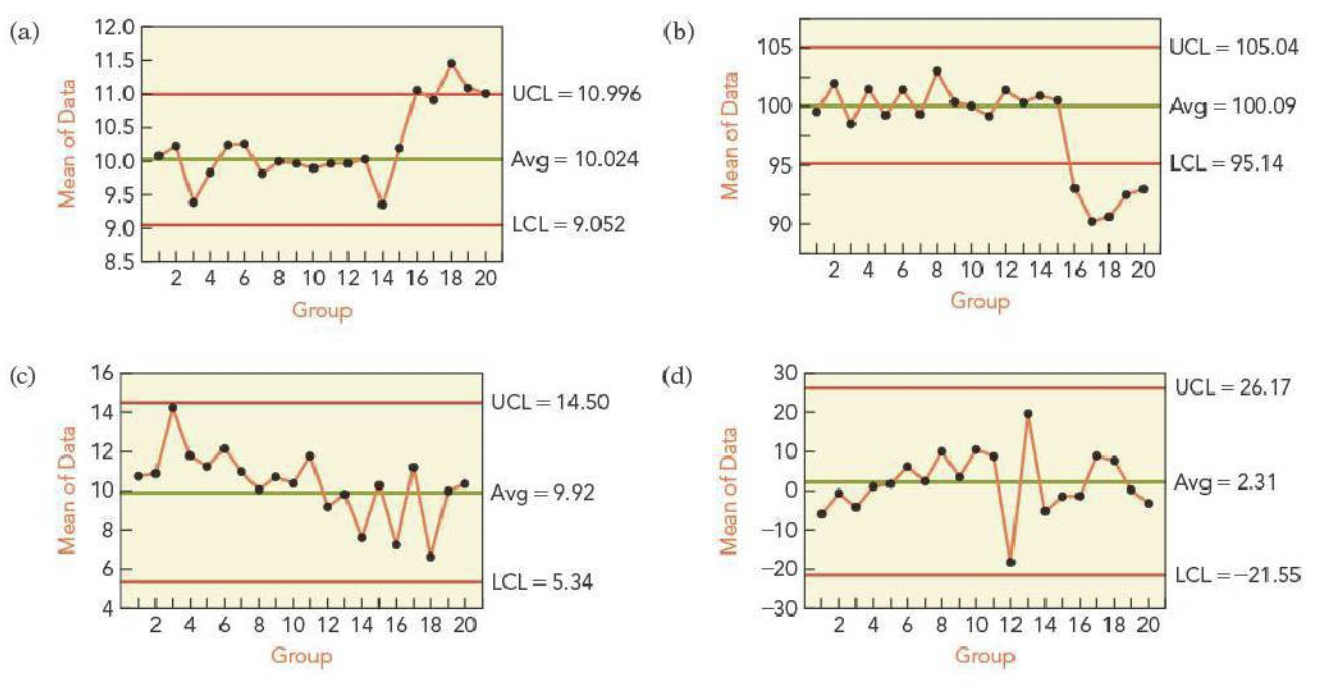
Which of the following $X$-bar charts show that a process went out of control?
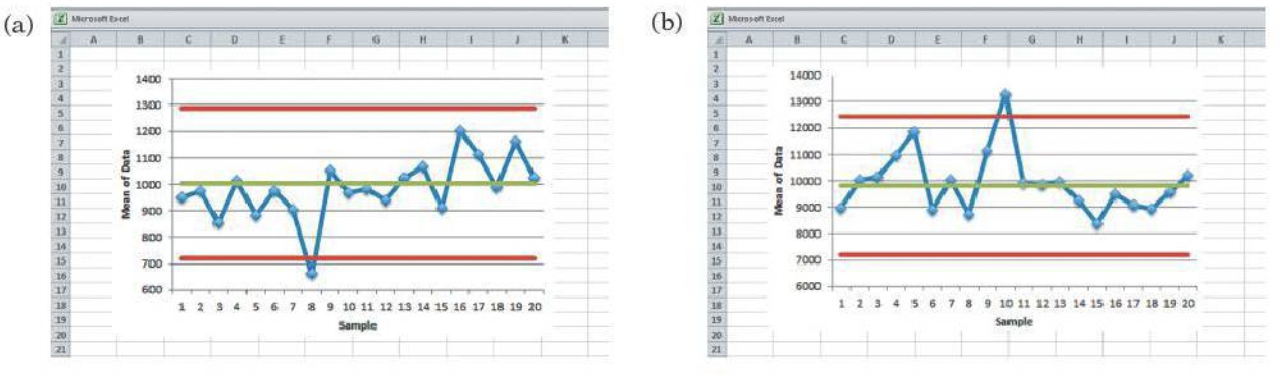
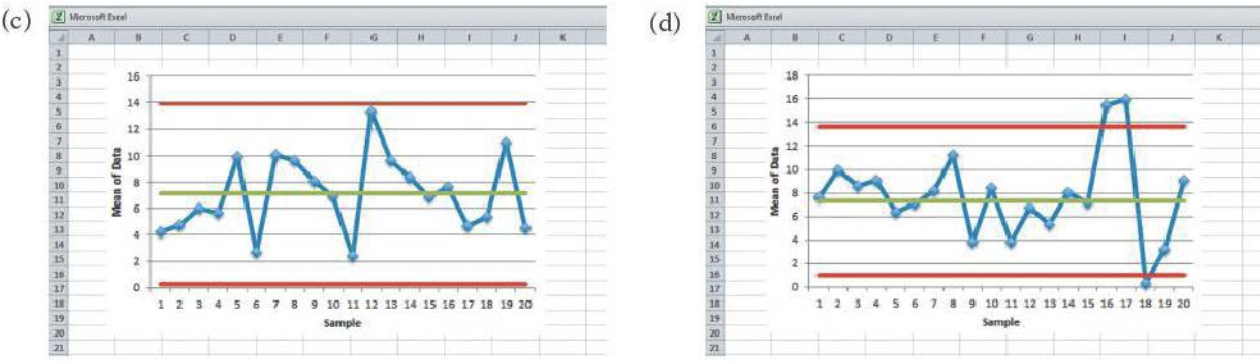
Which, if any, of these combinations of an $X$-bar and an $S$-chart suggest a problem? If there’s a problem, in which chart did you find the problem?
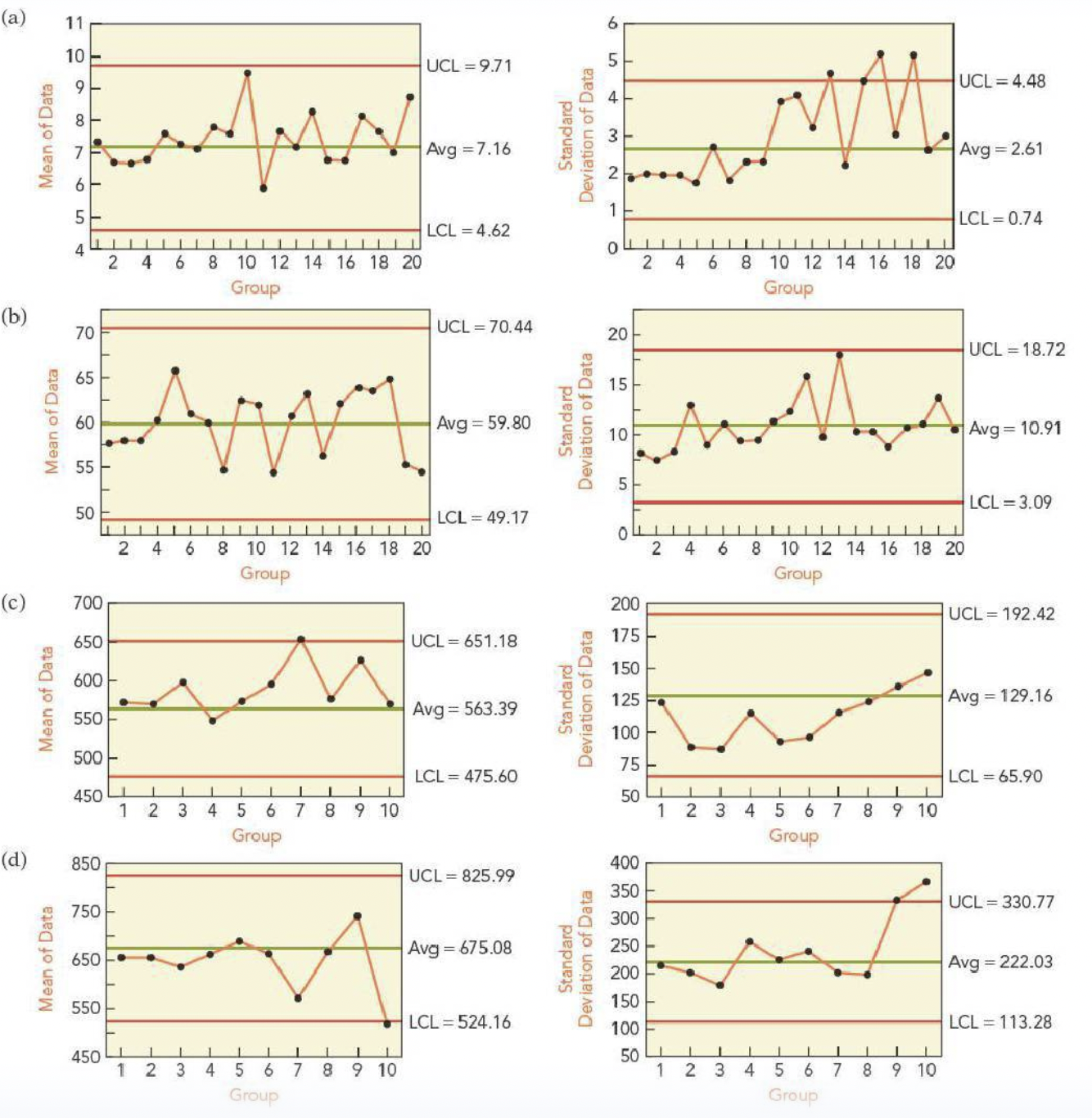
Which, if any, of these combinations of an $X$-bar and an $S$-chart suggest a problem? If there’s a problem, in which chart did you find the problem?
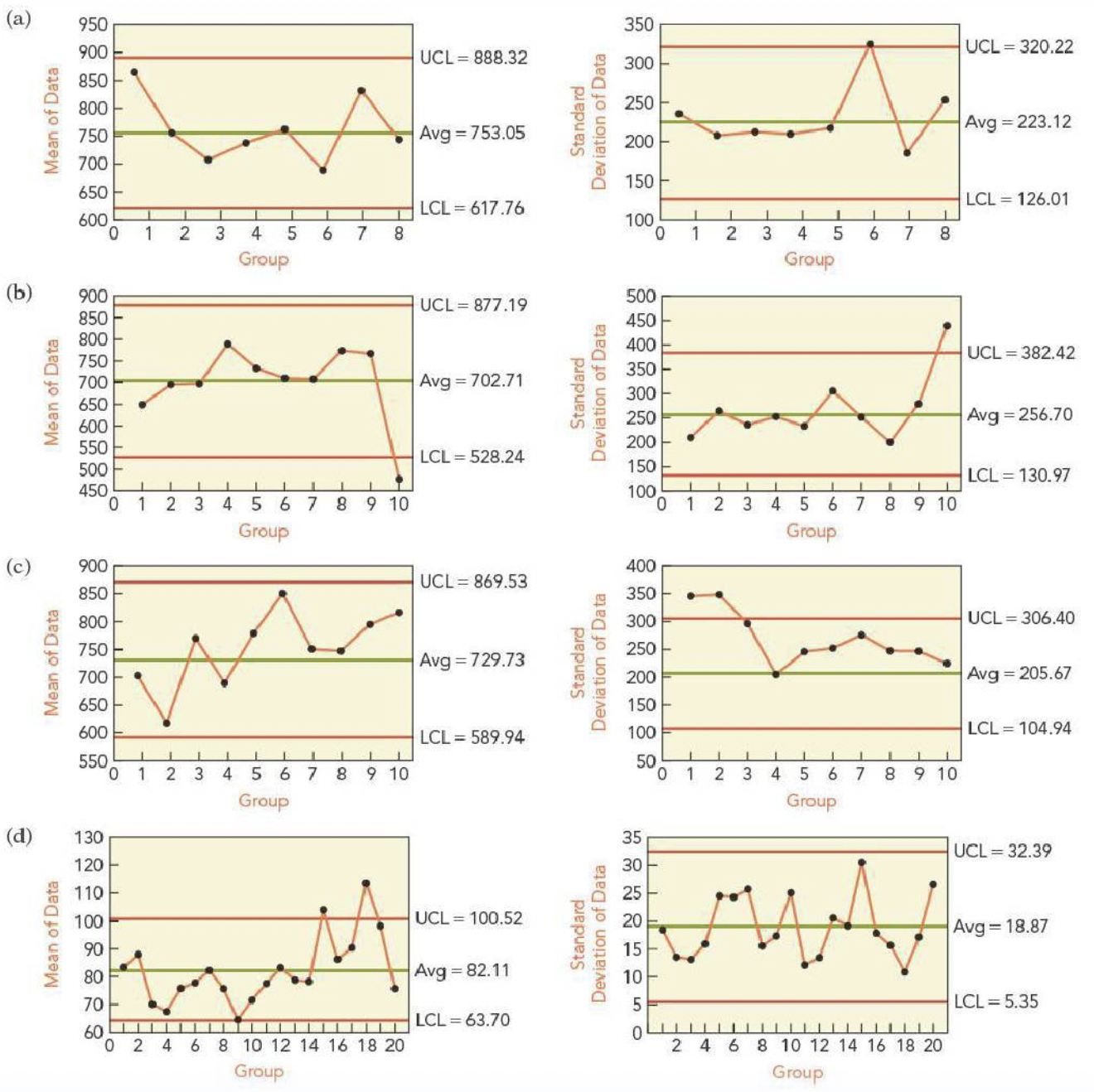
The manager of a warehouse monitors shipments. A random sample of 25 packages is selected and weighed every day. The mean weight should be $\mu = 22$ pounds, and $\sigma = 5$ pounds. True or False: An $X$-bar chart with control limits 12 pounds and 32 pounds has a 5% chance of a Type I error.
Rather than stop the production when a mean crosses the control limits in the $X$-bar chart, a manager has decided to wait until two consecutive means lie outside the control limits before stopping the process. The control limits are $\mu \pm 2\sigma/ \sqrt{n}$.
1. By waiting for two consecutive sample means to lie outside the control limits, has the manager increased or decreased the chance for a Type I error?
2. What is the probability of a Type I error if this procedure is used?
Where should the control limits for an $X$-bar chart be placed if the design of the process sets $\alpha = 0.0027$ with the following parameters (assume that the sample size condition for control charts has been verified)?
1. $\mu = 10, \sigma = 5,$ and $n = 18$ cases per batch
2. $\mu = -4, \sigma = 2,$ and $n = 12$ cases per batch

Expected value of \(X\)	a. \(E(X - \mu)\)
Variance of \(X\)	b. \(10X\)
Standard deviation of \(X\)	c. \(\frac{(X-0.04)}{\sigma}\)
Shorthand notation for \(P(X=x)\)	d. \(X+10\)
Has 10 times the standard deviation of \(X\)	e. \(E(X-\mu)^2\)
Is always equal to zero	f. \(\sqrt{VarX}\)
Increases the mean of \(X\) by 10	g. \(\mu\)
Has standard deviation 1	h. \(p(x)\)

Consequence of covariance	a. \(p(x,y)\)
Covariance between \(X\) and \(Y\)	b. \(\rho\)
Property of uncorrelated random variables	c. \(p(x, y) = p(x)p(y)\)
Weighted sum of two random variables	d. \(\rho\sigma_x\sigma_y\)
Sharpe ratio of random variable	e. \(Var(X+Y) >Var(X) + Var(Y)\)
Implies \(X\) and \(Y\) are independent random variables	f. \(p(x) = p(y)\)
Implies \(X\) and \(Y\) are identically distributed	g. \(X_1, X_2, X_3\)
Symbol for the correlation between random variables	h. \(Var(X+Y) = Var(X) + Var(Y)\)
Symbol for joint probability distribution	i. \(S(Y)\)
Sequence of iid random variables	j. \(3X-2Y\)

1. Expresssion for the variance of \(Y\)	a. \(np\)
Probability that the first trial \(B_1\) fails	b. \(e^{-\lambda}\)
Expression for the mean of \(X\)	c. \(e^{-\lambda} \frac{\lambda^2}{2}\)
Probability that \(Y\) is zero	d. \(p\)
Probability that \(X\) is 2	e. \(0\)
Covariance between \(B_1\) and \(B_2\)	f. \(p^n\)
Expression for the expected value of \(X\)	g. \(1-p\)
The expected value of \(B_1\)	h. \((1-p)^n\)
Probability that \(Y\) is \(n\)	i. \(np(1-p)\)
Probability that \(X\) is \(0\).	j. \(\lambda\)

Mean of \(X\)	a. \(\frac{1}{2}\)
Variance of \(X\)	b. \(P(Z<1)\)
Probability of \(X\) being less than its mean	c. \(0.05\)
Probability of \(X\) being less than \(\mu +\sigma\)	d. \(\frac{2}{3}\)
Standard deviation of \(Z\)	e. \(\frac{1}{1 googol}\)
Probability that a \(z-score\) based on \(X\) is less than \(1\) in magnitude	f. \(\mu\)
Proportion of a normal distribution that is more than \(20\sigma\) from \(\mu\)	g. \(\sigma^2\)
Difference between value of \(P(Z<-x)\) and value of \(P(Z>x)\)	h. \(1\)
Distribution of the random variable \(\mu +\sigma Z\)	i. \(0\)
Probability that \(Z>1.96\) plus the probability that \(Z<-1.96\)	j. \(N(\mu, \sigma^2)\)