03:00
Lec 5 - More probability rules
STAT 1010 - Fall 2022
Learning outcomes
By the end of this lesson you should:
Know and understand words like compliment, independent, and the Law of Large Numbers
Understand Boole’s inequality
Understand the multiplication and addition rules
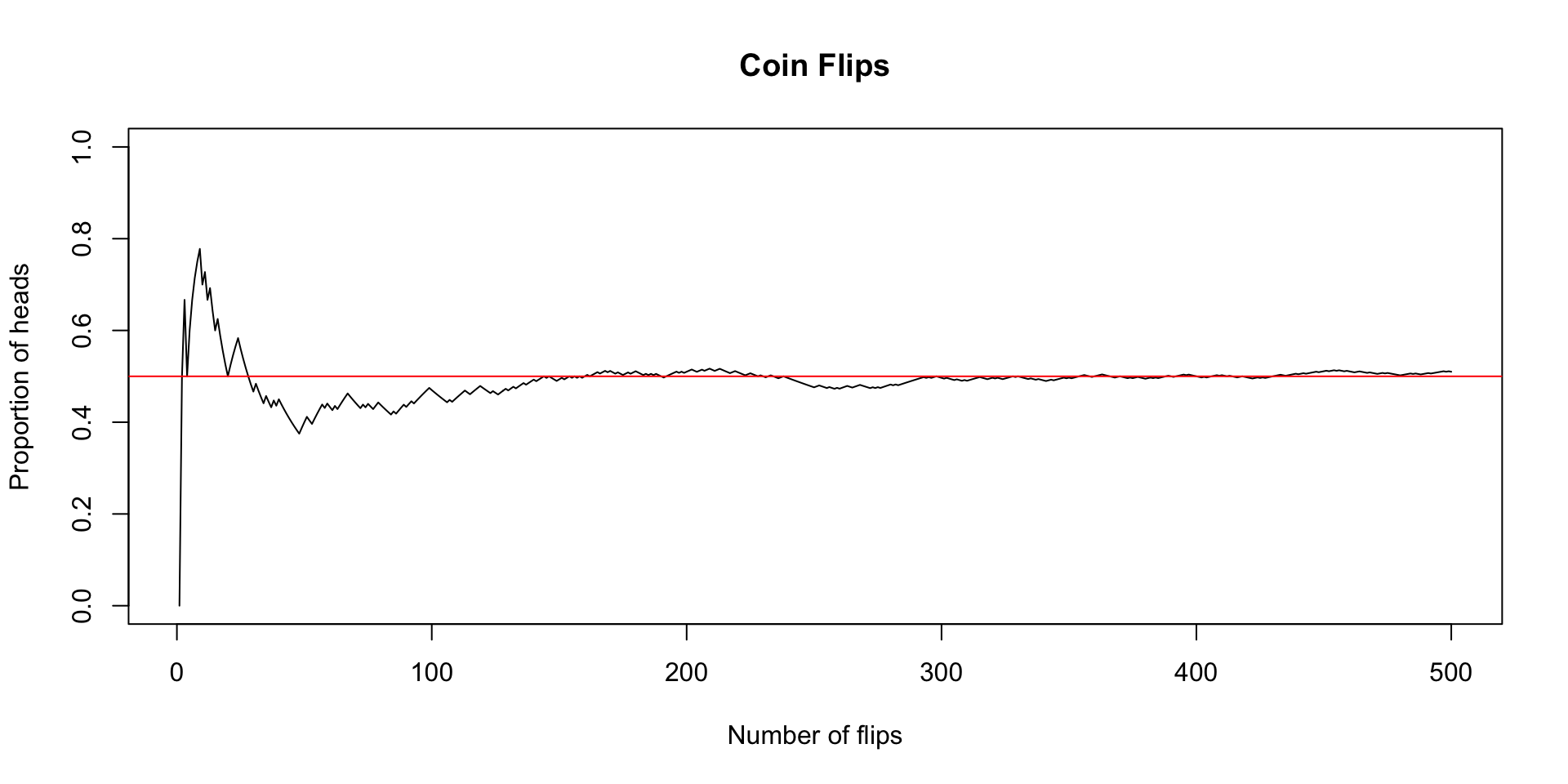
Law of large numbers (\(\infty\) in practice)
Compliment of \(A\)
\(S - A\)
Addition rule
\(Pr(A \cup B)=Pr(A)+Pr(B)−Pr(A \cap B)\)
Boole’s inequality
\(Pr(A \cup B) \leq Pr(A)+Pr(B)\)
Independent events
Events are said to be independent if the outcome of one event does not impact the probability of another.
Which of these events is independent?
- Removing balls from urns with replacement
- Removing balls from urns without replacement
- Flipping a coin ten times
- Riding in an uber and getting a free meal
- Going into a store and purchasing something from that store
- Suitability of two employees for a job
- Drawing 2 kings from a deck of cards in a row without replacement
3 mins
Conditional probability
When events are not independent conditional probabilities are useful.
We use the notation: \[Pr(Card\: 2\: is\: a\: king∣Card\: 1\: is\: a\: king)\] for this. We use the ∣ as shorthand for “given that” or “conditional on”.
Multiplication rule
\[Pr(A \cap B) = Pr(A)Pr(B∣A)\]
when \(A\) and \(B\) are independent, \(Pr(B|A)\) = ?
\(Pr(B|A) = Pr(B)\)
\(Pr(A \cap B) = Pr(A)Pr(B)\)
Tree diagrams
Your turn
Click here or the qr code below
